使用BLSTM结合Attention进行文本分类（Kaggle比赛Quora Insincere Questions Classification）

发表于 | 分类于 | 阅读次数：

参考文献一：Attention-Based Bidirectional Long Short-Term Memory Networks for Relation Classification
参考文献二：FEED-FORWARD NETWORKS WITH ATTENTION CAN SOLVE SOME LONG-TERM MEMORY PROBLEMS

本文中主要使用的是Bi-LSTM结合Attention进行文本分类。对于Bi-LSTM已经比较熟悉了，模型图可以参考下图，并不是本文的重点，本文的重点是Attention机制。

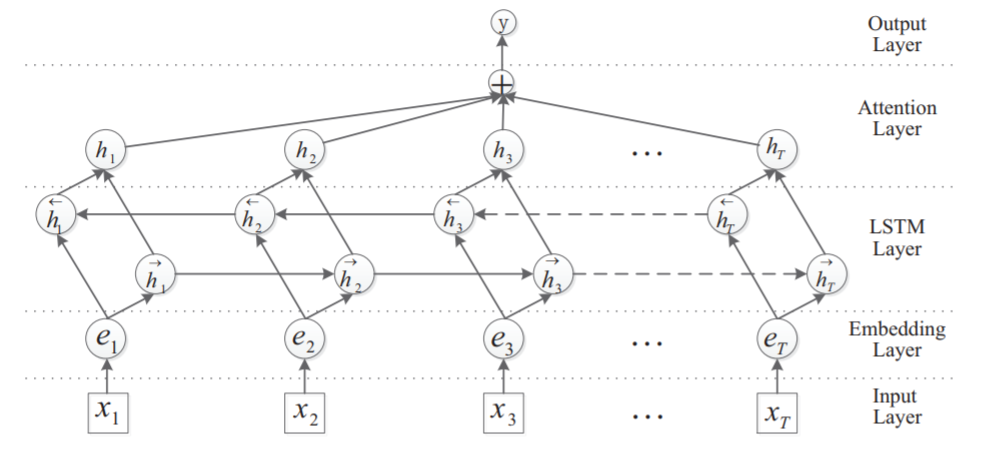
Alt text

关于Attention机制的原理在之前的博客中已经有提及了，我们再表达一遍：

对应上述公式，实现的代码主要是下面的函数，每个部分都加入了shape进行推导，应当是比较简单的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
def call(self, x, mask=None):
      # x.shape = (batch_size,timesteps,units)
      # W.shape=(units,)
      # eij.shape=(batch_size,timesteps)
      eij = dot_product(x, self.W)

      if self.bias:
          eij += self.b

      eij = K.tanh(eij)

      a = K.exp(eij)
      # in some cases especially in the early stages of training the sum may be almost zero
      # and this results in NaN's. A workaround is to add a very small positive number ε to the sum.
      # a.shape=(batch_size,timesteps)
      a /= K.cast(K.sum(a, axis=1, keepdims=True) + K.epsilon(), K.floatx())  # shape=(batch_size,timesteps,units)

      # x.shape = (batch_size,timesteps,units)
      # K.expand_dims(a).shape=(batch_size,timesteps,1)
      # weighted_input.shape=(batch_size,timesteps,units)
      # a = np.asarray([[1, 2, 3],[4, 5, 6]])
      # b = np.asarray([[2],[4]])
      # a * b = [[ 2,  4,  6],
      #          [16, 20, 24]]
      weighted_input = x * K.expand_dims(a)

      # result.shape=(batch_size,units)
      result = K.sum(weighted_input, axis=1)
      return result

对于整体的实现，首先可以参考编写你自己的 Keras 层，然后对照着这个文档，我们进行实现一个Attention类：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
from keras import backend as K, initializers, regularizers, constraints
from keras.engine.topology import Layer
from keras.layers import Embedding, Dense
from keras.models import Sequential


def dot_product(x, kernel):
    """
    Wrapper for dot product operation, in order to be compatible with both
    Theano and Tensorflow
    Args:
        x (): input
        kernel (): weights
    Returns:
    """
    if K.backend() == 'tensorflow':
        # todo: check that this is correct
        return K.squeeze(K.dot(x, K.expand_dims(kernel)), axis=-1)
    else:
        return K.dot(x, kernel)


class Attention(Layer):
    def __init__(self,
                 W_regularizer=None, b_regularizer=None,
                 W_constraint=None, b_constraint=None,
                 bias=True,
                 return_attention=False,
                 **kwargs):
        """
        Keras Layer that implements an Attention mechanism for temporal data.
        Supports Masking.
        Follows the work of Raffel et al. [https://arxiv.org/abs/1512.08756]
        # Input shape
            3D tensor with shape: `(samples, steps, features)`.
        # Output shape
            2D tensor with shape: `(samples, features)`.
        :param kwargs:
        Just put it on top of an RNN Layer (GRU/LSTM/SimpleRNN) with return_sequences=True.
        The dimensions are inferred based on the output shape of the RNN.


        Note: The layer has been tested with Keras 1.x

        Example:
        
            # 1
            model.add(LSTM(64, return_sequences=True))
            model.add(Attention())
            # next add a Dense layer (for classification/regression) or whatever...

            # 2 - Get the attention scores
            hidden = LSTM(64, return_sequences=True)(words)
            sentence, word_scores = Attention(return_attention=True)(hidden)

        """
        self.supports_masking = True
        self.return_attention = return_attention
        self.init = initializers.get('glorot_uniform')

        self.W_regularizer = regularizers.get(W_regularizer)
        self.b_regularizer = regularizers.get(b_regularizer)

        self.W_constraint = constraints.get(W_constraint)
        self.b_constraint = constraints.get(b_constraint)

        self.bias = bias
        super(Attention, self).__init__(**kwargs)

    def build(self, input_shape):
        assert len(input_shape) == 3

        self.W = self.add_weight((input_shape[-1],),
                                 initializer=self.init,
                                 name='{}_W'.format(self.name),
                                 regularizer=self.W_regularizer,
                                 constraint=self.W_constraint)
        if self.bias:
            self.b = self.add_weight((input_shape[1],),
                                     initializer='zero',
                                     name='{}_b'.format(self.name),
                                     regularizer=self.b_regularizer,
                                     constraint=self.b_constraint)
        else:
            self.b = None

        self.built = True

    def compute_mask(self, input, input_mask=None):
        # do not pass the mask to the next layers
        return None

    def call(self, x, mask=None):
        # x.shape = (batch_size,timesteps,units)
        # W.shape=(units,)
        # eij.shape=(batch_size,timesteps)
        eij = dot_product(x, self.W)

        if self.bias:
            eij += self.b

        eij = K.tanh(eij)

        a = K.exp(eij)

        # apply mask after the exp. will be re-normalized next
        if mask is not None:
            # Cast the mask to floatX to avoid float64 upcasting in theano
            a *= K.cast(mask, K.floatx())

        # in some cases especially in the early stages of training the sum may be almost zero
        # and this results in NaN's. A workaround is to add a very small positive number ε to the sum.
        # a /= K.cast(K.sum(a, axis=1, keepdims=True), K.floatx())
        # a.shape=(batch_size,timesteps)
        a /= K.cast(K.sum(a, axis=1, keepdims=True) + K.epsilon(), K.floatx())  # shape=(batch_size,timesteps,units)

        # x.shape = (batch_size,timesteps,units)
        # K.expand_dims(a).shape=(batch_size,timesteps,1)
        # weighted_input.shape=(batch_size,timesteps,units)
        # a = np.asarray([[1, 2, 3],[4, 5, 6]])
        # b = np.asarray([[2],[4]])
        # a * b = [[ 2,  4,  6],
        #          [16, 20, 24]]
        weighted_input = x * K.expand_dims(a)

        # result.shape=(batch_size,units)
        result = K.sum(weighted_input, axis=1)
        if self.return_attention:
            return [result, a]
        return result

    def compute_output_shape(self, input_shape):
        if self.return_attention:
            return [(input_shape[0], input_shape[-1]),
                    (input_shape[0], input_shape[1])]
        else:
            return input_shape[0], input_shape[-1]

最终这个代码我们就可以用在我们的文本分类模型上了。